The Friendship Paradox

About 20 years ago, a sociologist named Scott Feld discovered an interesting phenomenon where on the average, people have less friends than their friends do.  However, most people believe they have more friends than their friends do.  This is the paradox.  The friendship paradox is a form of sampling bias.
What is a sampling bias?  Let’s say you want to find out what the maximum weight an average person can bench press is. You interview everyone at the gym and find out the average is 220 pounds. Yours is only 150. Should you feel bad? Probably not, because this is a biased experiment. You would need to include answers from exactly the type of people who don’t show up in a gym to get a better representation of the entire population.  By only asking people already at the gym, you are only including results of the people who are most likely to have a high bench press.
Scientists are allowed to draw conclusions from samples to represent entire populations.  They can do this because of the central limit theorem and law of averages.  However, the trick is making sure your sample is indeed a good representation of the population.  Sampling biases distort this representation.
Likewise, the sample is weighted towards the extremes in a large enough social graph: people who have a lot of friends. You’re simply more likely to be friends with people who have friends than those that don’t.
We can illustrate this with an example. Let’s consider this small group of people:

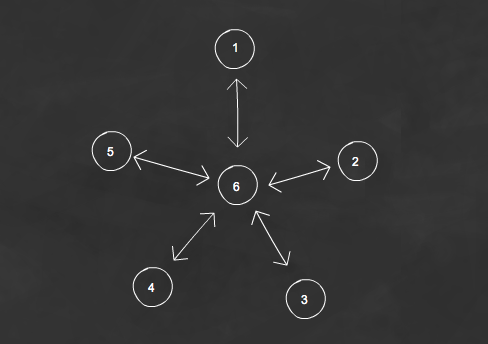
Each of these circles represent a person and the lines represent their friendships. If you count the lines for every individual person, you’ll find there are 10 bidirectional friendships here. (we’re assuming you can’t be friends with someone else without them knowing it.)
1,2,3,4,5 are all friends with 6
6 is all friends with 1,2,3,4,5.  So, 10 friendships total.
We find there is an average of 1.67 friends per person. (10 friendships / 6 people)
Now if you were to ask everyone here how many friends they have, five out of six will tell you they have 1 friend, which is less than the average. While it may not be true in every instance, there have been experiments conducted to test the validity of this idea on a large scale. 721 million Facebook users and their 69 billion friendships were examined and the friendship paradox held up for 93% of all 721 million people. Users averaged 190 friends while their friends averaged 690 friends. (Illustrated in this piece by the NYT)
The friendship paradox also has some interesting practical applications. It has been used before to identify individuals in a network that are likely to be conduits of disease to the highest amount of people. Being able to accurately forecast these allows us to slow or even prevent epidemics from spreading by identifying the right types of people to immunize first.
This type of prediction is so strong and reliable that in one study it was able to detect flu outbreaks almost 2 weeks earlier than what traditional measures are able to.